chatgpt专题
标注
定位
正则表达式
ratio-test
MCAL
社区论坛
synchronized
supervisor
自动批量下载图片的插件
photoshop
定时同步
Conditional注解
分库分表
对象
磁盘
onenet
SoftReference
阈值
加锁原理
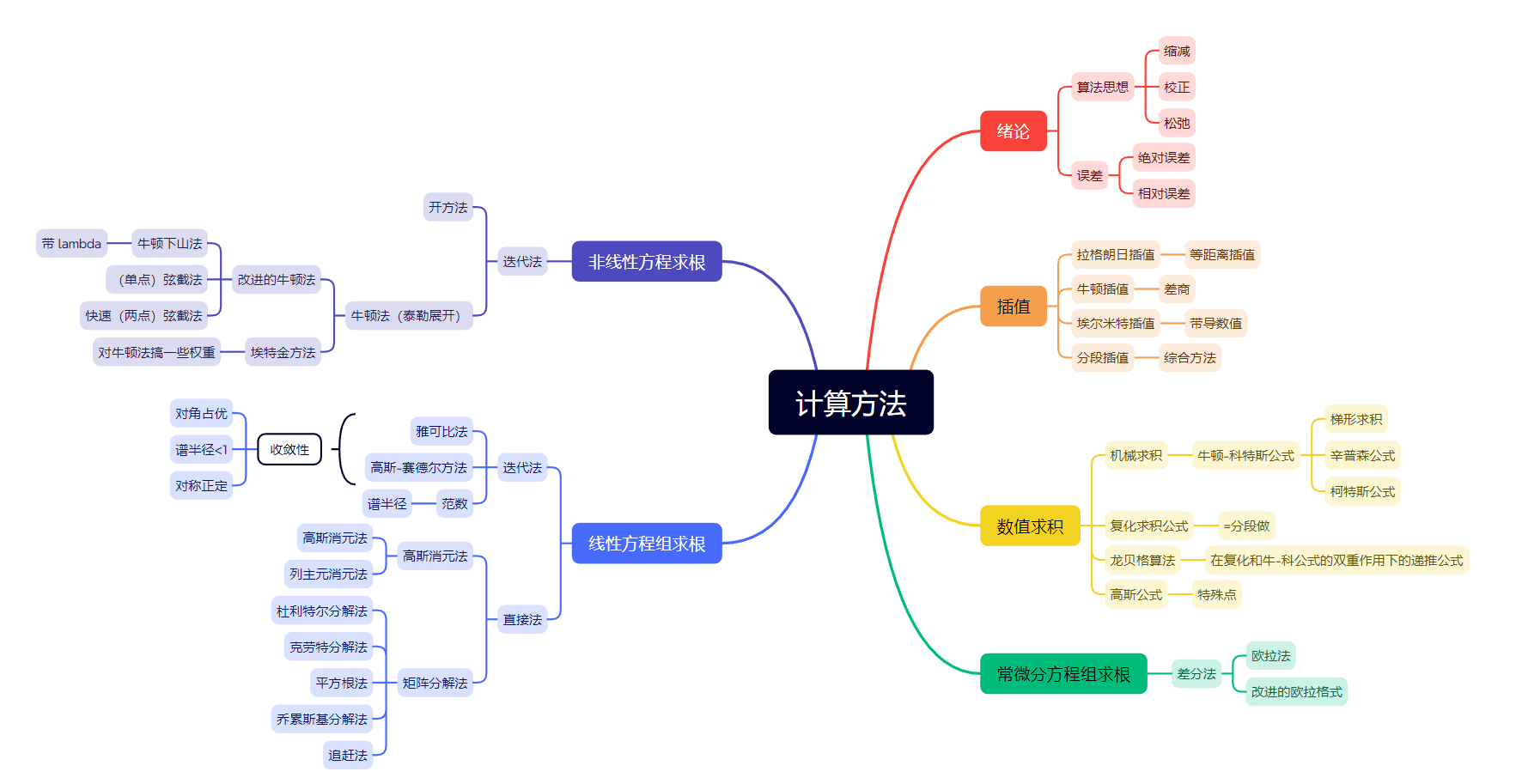
数值分析
2024/4/11 19:45:20均匀节点插值与切比雪夫插值以及龙格现象
import numpy as np
import matplotlib.pyplot as pltdef inter_x(a, b, n):""":param a: 插值区间左端点:param b: 插值区间右端点:param n: 插值点个数:return: 插值节点向量"""x np.zeros(n1)h (b - a) / nfor i in range(n1):x[i] a i *…
数值分析学习笔记——误差【华科B站教程版本】
误差
误差:一个物理量的真实值与计算值之间的误差
误差来源与分类
模型误差:对问题所抽象出来的数学/物理模型是误差的,比如要有一些假设条件才进行理论的推导观测误差:测量得到的模型的参数的值的误差方法误差(截断…
Jacobi迭代法和Gauss-Seidel迭代法的收敛性
Axb
系数矩阵A按行严格对角占优
若系数矩阵A按行严格对角占有>Jacobi迭代法和Gauss-Seidel迭代法均收敛
迭代矩阵B谱半径<1
Jacobi迭代法和Gauss-Seidel迭代法收敛<>迭代矩阵B的谱半径<1 其中,Jacobi迭代法的迭代矩阵 B − D − 1 ( L U ) B-D…
高等数值计算方法学习笔记第4章第二部分【数值积分(数值微分)】
高等数值计算方法学习笔记第4章第二部分【数值积分(数值微分)】四、龙贝格求积公式(第三次课)1.梯形法的递推化 (变步长求积法)2.龙贝格算法五、高斯求积公式1.一般理论(1定义1例题)2.构造高斯求积公式方法(二…
向量形式四阶龙格库塔法的仿真细节
摘要 给出了四阶龙格库塔法(ODE4)的向量形式,推导了二阶积分器串联型系统的ODE4更新公式,解释了在使用ODE4仿真高阶系统和带外部输入系统时的各种注意事项,最后给出四阶龙格库塔法只能使用一次的重要结论。
标量和向量…
数值分析学习笔记——绪论【华科B站教程版本】
绪论
数值分析概念
用计算机求解数学问题的数值方法和理论
三大科学研究方法
实验理论分析科学计算(用计算机去辅助研究):数值方法计算机
解析解和近似解
解析解:使用数学方法求出或推导出的结果,往往可以求解出…
数值计算方法课程笔记02
数值计算方法课程笔记02内容预览笔记笔记内容为日常上课记录与整理,为图片格式,仅供学习。 内容预览
01.非线性方程求根 02.牛顿下山法 03.线性方程组的直接解法 04.高斯消去法 05.高斯主元消去法 06.列主元消去法 07.全主元消去法 08.列主元高斯-约当消…
【数值分析】1 - 误差及有关概念
文章目录 一、误差的背景介绍1.1 误差的来源与分类1.2 误差的传播与积累1.3 例题1.3.1 公式一1.3.2 公式二1.3.3 总结 二、误差与有效数字2.1 绝对误差与绝对误差限2.2 相对误差和相对误差限 三、有效数字3.1 有效数字的定义和标准浮点式3.1.1 例题 3.2 有效数字与相对误差的关…
数值计算(二)——插值计算(1)拉格朗日插值法
插值问题
设函数fff定义在[a,b][a,b][a,b]上,设x1,x2,...,xn∈[a,b]x_1,x_2,...,x_n\in[a,b]x1,x2,...,xn∈[a,b]是n1n1n1个相异节点,令yif(xi),i0,1,...,ny_if(x_i),i0,1,...,nyif(xi),i0,1,...,n插值法就是构造一个便于计算的简单函数φ\va…
【数值分析】逼近,正交多项式
逼近
由离散点(函数表)给出函数关系通常有两种方法:
使用多项式插值 使用多项式插值会带来两个问题:1. 龙格现象2. 数值本身带有误差,使用插值条件来确定函数关系不合理三次样条插值 三次样条插值克服了龙格现象&…
非线性方程求根法(python实现)
非线性方程求根
import numpy as npdef bisect(f, a, b, tol):""":param f: 非线性函数:param a: 区间左端点:param b: 区间右端点:param tol: 误差容忍范围:return: 非线性函数在[a,b]上的根"""if np.sign(f(a) * f(b)) > 0: # wrong inp…
【数值分析】反幂法,matlab实现
反幂法20231226
一种求实矩阵 A {A} A 的按模最小的特征值,及其对应的特征向量 x i {x_i} xi 的方法,只能求一个。 要保证矩阵最小特征值只有一个,有 n {n} n 个线性无关的特征向量,矩阵可逆。 可以通过求矩阵 A − 1 {A^{…
【校招VIP】常用产品分析之数值分析能力
考点介绍: 产品的生命周期各个阶段都伴随着产品数据的变化,产品经理根据这些数据来判断产品所在阶段并对后期的产品演进进行合理的规划;在产品需求分析阶段,通过数据分析来鉴别用户需求的真伪;在产品上线后,…
数值分析第四章节 用Python实现数值积分与数值微分
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第4章 数值积分与数值微分 文章声明:如有发现错误,欢迎批评指正 文章目录 梯形公式矩形公式辛普森公式柯特斯公式复合梯形公式复合辛普森公式 4.1数值积分概论 4.1.1数值积分基本思想 使用某…
【数值分析】区间折半法,matlab实现
区间折半法
从梯形公式出发,上一步步长为 h {h} h ,则有步长折半后的积分 T 2 n 1 2 T n h 2 ∑ i 0 n − 1 f ( x i 0.5 ) T_{2n} \frac{1}{2}T_n \frac{h}{2} \sum_{i0}^{ n-1}f(x_{i0.5}) T2n21Tn2hi0∑n−1f(xi0.5) matlab实现
…
数值分析复习:逼近理论的应用——最小二乘问题、解超定、欠定方程组
文章目录 逼近理论的应用——最小二乘问题、解超定、欠定方程组离散平方逼近最小二乘解 本篇文章适合个人复习翻阅,不建议新手入门使用 本专栏:数值分析复习 的前置知识主要有:数学分析、高等代数、泛函分析 逼近理论的应用——最小二乘问题、…
【数值分析】2 - 插值法
文章目录 一、引言1.1 插值法引入1.2 常用插值法1.3 插值法定义 二、插值法研究的问题2.1 插值多项式存在的唯一性2.2 如何构造n次多项式2.2.1 待定系数法2.2.2 拉格朗日插值法2.2.2.1 拉格朗日多项式2.2.2.2 拉格朗日插值余项2.2.2.3 例题2.2.2.4 拉格朗日插值法的问题 2.2.3 …
计算机中实数的浮点表示
最近开始看数值分析的书籍,在此做些笔记!
本节介绍一个关于浮点数的计算机计算模型IEEE 754浮点标准。IEEE(电器和电子工程师协会)对于建立行业标准有着积极的兴趣,他们的浮点运算格式已经成为整个计算机行业中单精度和双精度运算的共同标准…
数值方法算法实现[MATLAB语言]
MATLAB计算方法算法代码❤️❤️1. LU分解💙函数文件.m💚测试脚本.m💜测试结果❤️❤️2. Gauss消元💙函数文件.m💚测试脚本.m💜测试结果❤️❤️3. 平方根法💙函数文件.m💚测试脚本…
【数值分析】非线性方程求根,牛顿法,牛顿下山法,matlab实现
4. 牛顿法
收敛时牛顿法的收敛速度是二阶的,不低于二阶。如果函数有重根,牛顿法一般不是二阶收敛的。 x k 1 x k − f ( x k ) f ′ ( x k ) x_{k1}x_k- \frac{f(x_k)}{f(x_k)} xk1xk−f′(xk)f(xk) matlab实现
%% 牛顿迭代例子
f (x) x…
第九章节 用Python实现常微分方程初值问题的数值解法
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第9章 常微分方程初值问题的数值解法 文章声明:如有发现错误,欢迎批评指正 文章目录 欧拉法后退的欧拉方法梯形方法改进欧拉公式补充龙格—库塔方法线性多步法阿当姆斯显示与隐式公式 9.1引…
Python实现牛顿迭代法
1.题目 2.代码
import sympy as sy
def fx_Value(x0, fx):result fx.subs(x, x0)return resultdef Newton(x0, fx, e1e-6):# fx是原函数# x0是初值# e是误差
times 0while True:x_buff x0x0 x0 - fx_Value(x0, fx) / fx_Value(x0, sy.diff(fx))times 1if abs(x0 - x_buff…
python实现雅克比(Jacobi)迭代法
import numpy as np
#e为误差
def Jacobi(A,b,x,e,times100):length, width np.shape(A)D np.mat(np.diag(np.diag(A)))L np.triu(A, 1)U np.tril(A, -1)J -D.I * (L U)H np.eye(length) - D.I * Aeig,_ np.linalg.eig(H)spectral_radius max(abs(eig))if spectral_ra…
Python实现第一型三次样条插值函数
例题 代码
import numpy as np
np.set_printoptions(suppressTrue)def h_u_lamb_A(x):h []u []lamb []nx.shape[0]A np.mat(2*np.eye(n-2, n-2))A[0, 1] 1A[n-3, n-4] 1for i in range(0, n - 3):h.append(x[i 2] - x[i1])for i in range(0, n - 4):u.append(h[i] / (h…
python实现SOR迭代法
照着上面的式子写
def SOR(A,b,x,e,w,times100):#A为方程组系数矩阵#b为右端向量#x为初始解#e为误差大小#w为松弛因子#times为迭代次数D np.mat(np.diag(np.diag(A)))L np.triu(A, 1)U np.tril(A, -1)Sw (Dw*L).I*((1-w)*D-w*U)fw w*((Dw*L).I)*bx0xx Sw * x0 fwk 1w…
迭代法求解非线性方程的根
不动点迭代法求解非线性方程的根知识储备解题要点KaTeX数学公式知识储备
1、求解的是非线性方程放f(x)0的根
解题要点
1、判断使用全局收敛性定理还是局部收敛性定理
全局收敛性:未知根,已知根的取值区间(定理1.1/1.2)
局部收…
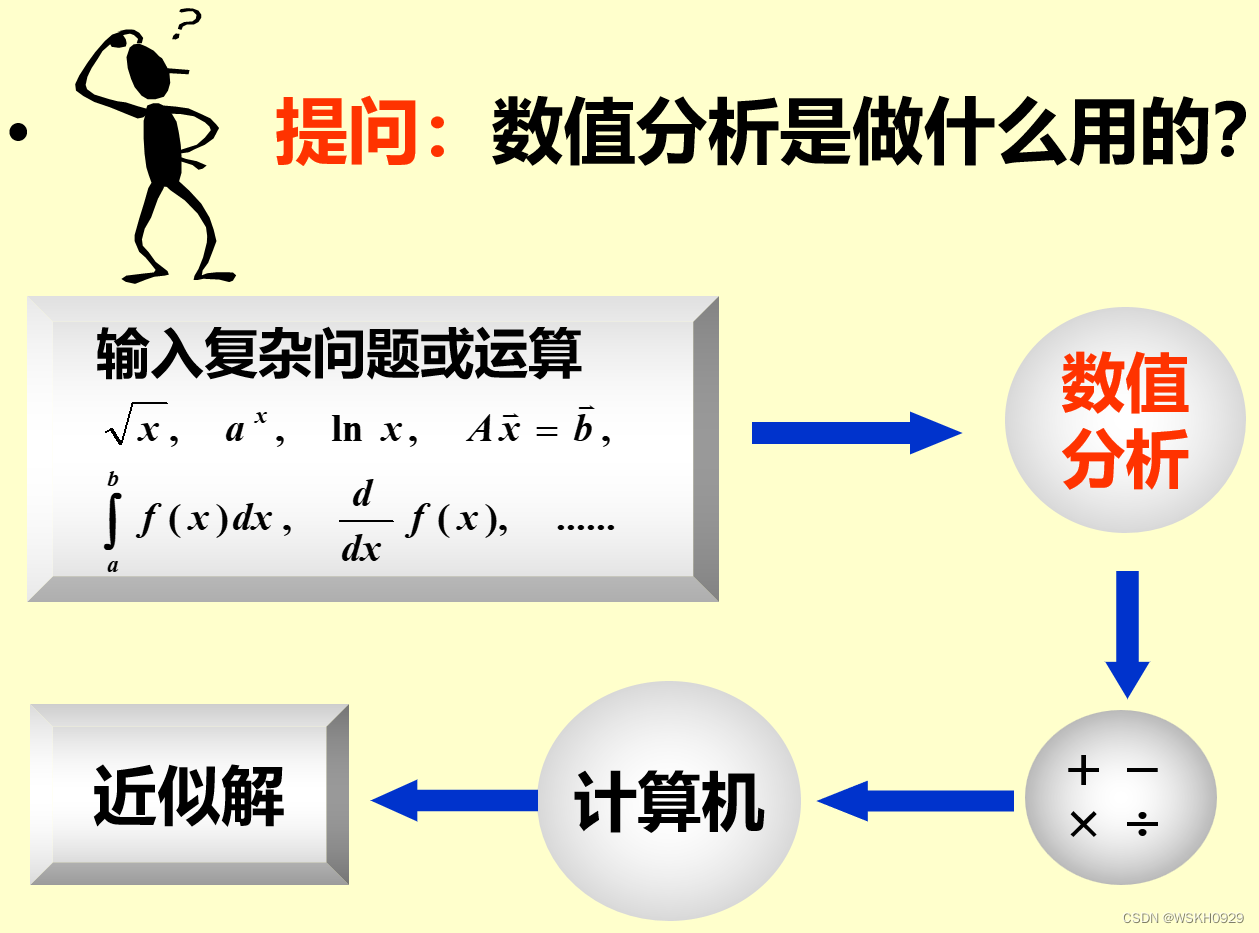
【数值分析】0 - 数值分析绪论
文章目录 一、数值分析介绍二、数值分析应用2.1 解三角函数2.2 计算多项式2.3 解线性方程组2.4 供水计划和生产调度计划的制定2.5 湘江水流量估计的实际意义2.6 机器学习或大数据 三、数值分析内容四、数值分析参考书目 学习视频:《数值分析》| 华科 | 研究生基础课…




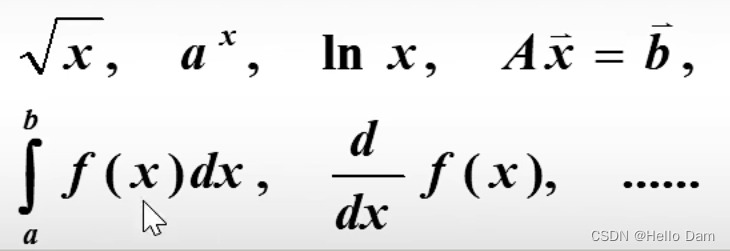









![数值方法算法实现[MATLAB语言]](https://img-blog.csdnimg.cn/0e64d95086934b31b3d87c213c7c6e60.png)